译 | 什么是深度学习里的卷积?
近年来,随着一些强大、通用的深度学习框架相继出现,把卷积层添加进深度学习模型也成了可能。这个过程很简单,只需一行代码就能实现。但是,你真的理解“卷积”是什么吗?当初学者第一次接触这个词时,看到堆叠在一起的卷积、核、通道等术语,他们往往会感到困惑。作为一个概念,“卷积”这个词本身就是复杂、多层次的。
在这篇文章中,我们将分解卷积操作的机制,逐步将其与标准神经网络联系起来,探索它们是如何建立起强大的视觉层次结构,并最终成为强大的图像特征提取器的。
2D卷积:操作
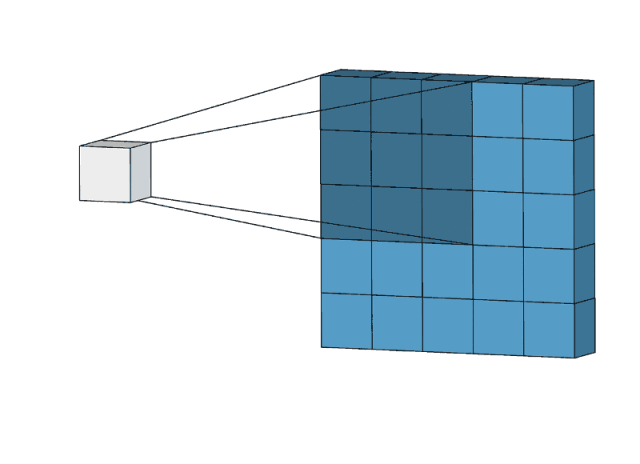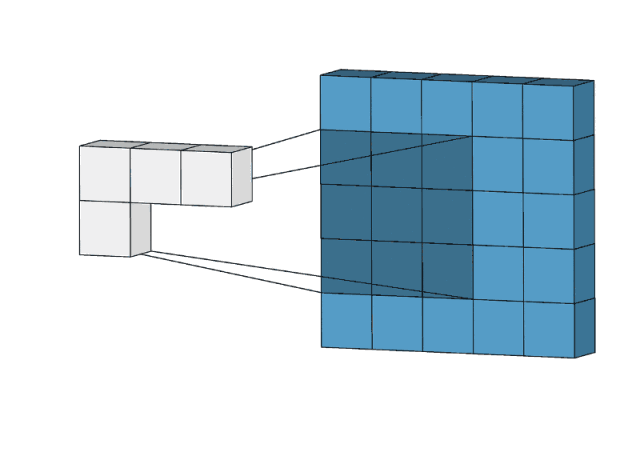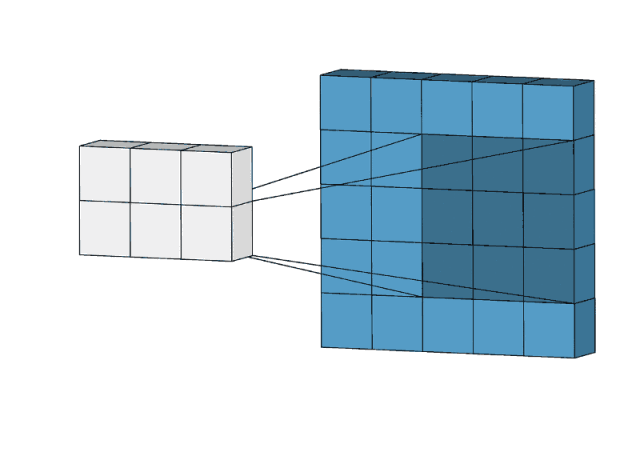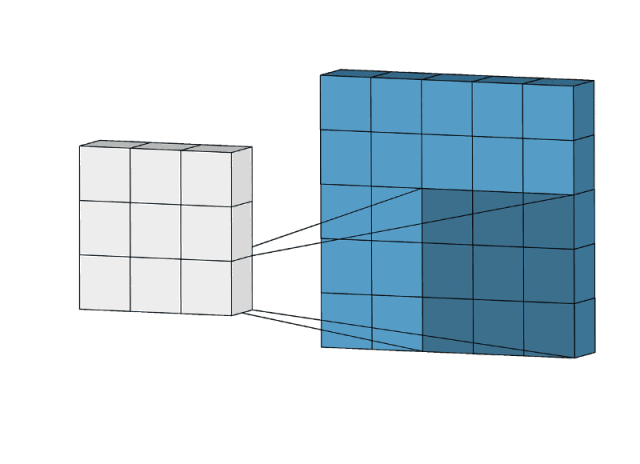
2D卷积是一个相当简单的操作:我们先从一个小小的权重矩阵,也就是卷积核(kernel)开始,让它逐步在二维输入数据上“扫描”。卷积核“滑动”的同时,计算权重矩阵和扫描所得的数据矩阵的乘积,然后把结果汇总成一个输出像素。

标准卷积
卷积核会在其经过的所有位置上都重复以上操作,直到把输入特征矩阵转换为另一个二维的特征矩阵。简而言之,输出的特征基本上就是原输入特征的加权和(权重是卷积核自带的值),而从像素位置上看,它们所处的地方大致相同。
那么为什么输出特征的会落入这个“大致区域”呢?这取决于卷积核的大小。卷积核的大小直接决定了在生成输出特征时,它合并了多少输入特征,也就是说:卷积核越小,输入输出的位置越接近;卷积核越大,距离就越远。
 这和全连接层很不一样。在上图的例子中,我们的输入有5×5=25个特征,而我们的输出则是3×3=9个特征。如果这是一个全连接层,输入25个特征后,我们会输出包含25×9=225个参数的权重矩阵,每个输出特征都是每个输入特征的加权和。
这和全连接层很不一样。在上图的例子中,我们的输入有5×5=25个特征,而我们的输出则是3×3=9个特征。如果这是一个全连接层,输入25个特征后,我们会输出包含25×9=225个参数的权重矩阵,每个输出特征都是每个输入特征的加权和。
这意味着对于每个输入特征,卷积执行的操作是使用9个参数进行转换。它关注的不是每个特征究竟是什么,而是这个大致位置都有什么特征。这一点很重要,理解了它,我们才能进行深入探讨。
一些常用的技巧
在我们继续讨论前,我们先来看看卷积神经网络中经常出现的两种技巧:Padding和Strides。
Padding
如果你仔细看了上文中的gif,你会发现我们把5×5的特征矩阵转换成了3×3的特征矩阵,输入图像的边缘被“修剪”掉了,这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。这是不理想的,通常我们都希望输入和输出的大小应该保持一致。
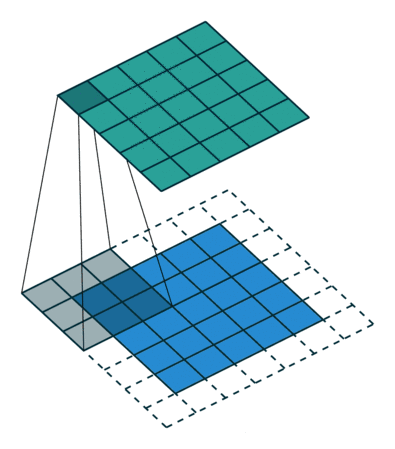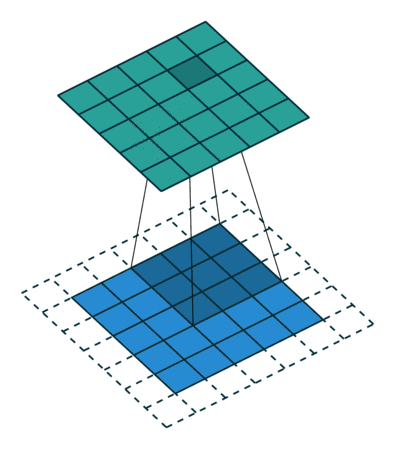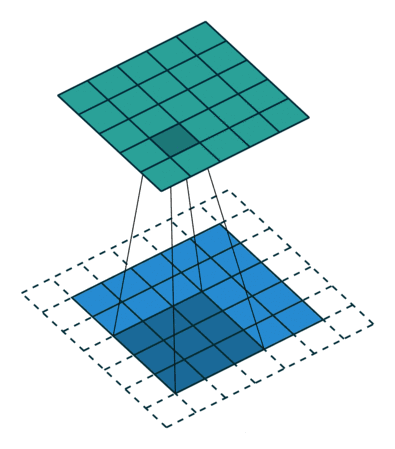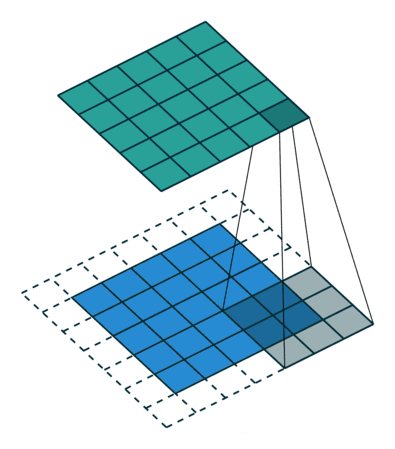
padding
Padding就是针对这个问题提出的一个解决方案:它会用额外的“假”像素填充边缘(值一般为0),这样,当卷积核扫描输入数据时,它能延伸到边缘以外的伪像素,从而使输出和输入大小相同。
Stride
如果说Padding的作用是使输出与输入同高宽,那么在卷积层中,有时我们会需要一个尺寸小于输入的输出。那这该怎么办呢?这其实是卷积神经网络中的一种常见应用,当通道数量增加时,我们需要降低特征空间维度。实现这一目标有两种方法,一是使用池化层,二是使用Stride(步幅)。
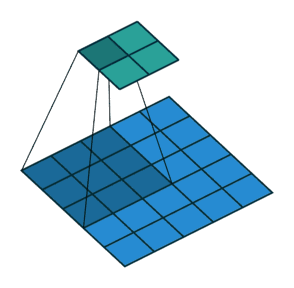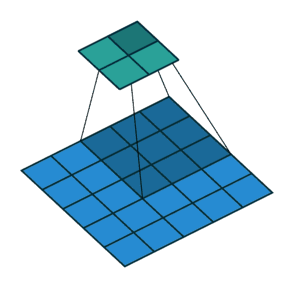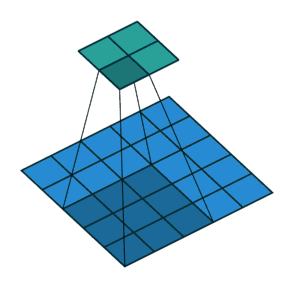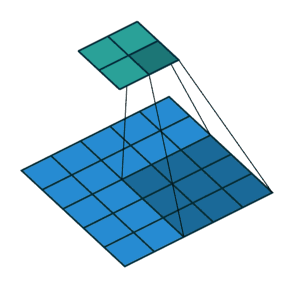
步幅
滑动卷积核时,我们会先从输入的左上角开始,每次往左滑动一列或者往下滑动一行逐一计算输出,我们将每次滑动的行数和列数称为Stride,在上节的图片中,Stride=1;在上图中,Stride=2。Stride的作用是成倍缩小尺寸,而这个参数的值就是缩小的具体倍数,比如步幅为2,输出就是输入的1/2;步幅为3,输出就是输入的1/3。以此类推。
在一些目前比较先进的网络架构中,如ResNet,它们都选择使用较少的池化层,在有缩小输出需要时选择步幅卷积。
多通道卷积
当然,上述例子都只包含一个输入通道。实际上,大多数输入图像都有3个RGB通道,而通道数的增加意味着网络深度的增加。为了方便理解,我们可以把不同通道看成观察全图的不同“视角”,它或许会忽略某些特征,但一定也会强调某些特征。

彩色图像一般都有红、绿、蓝三个通道
这里就要涉及到“卷积核”和“filter”这两个术语的区别。在只有一个通道的情况下,“卷积核”就相当于“filter”,这两个概念是可以互换的;但在一般情况下,它们是两个完全不同的概念。每个“filter”实际上恰好是“卷积核”的一个集合,在当前层,每个通道都对应一个卷积核,且这个卷积核是独一无二的。
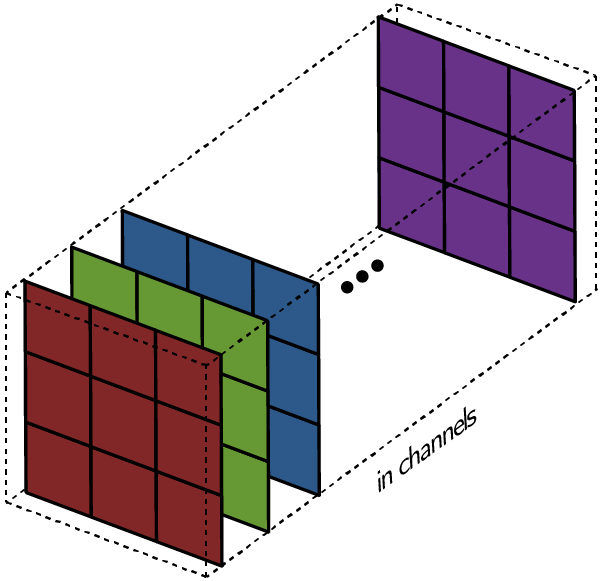
filter:卷积核的集合
卷积层中的每个filter有且只有一个输出通道——当filter中的各个卷积核在输入数据上滑动时,它们会输出不同的处理结果,其中一些卷积核的权重可能更高,而它相应通道的数据也会被更加重视(例:如果红色通道的卷积核权重更高,filter就会更关注这个通道的特征差异)。
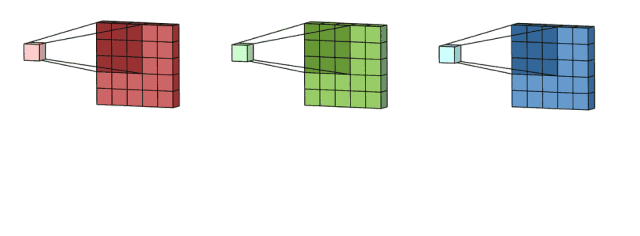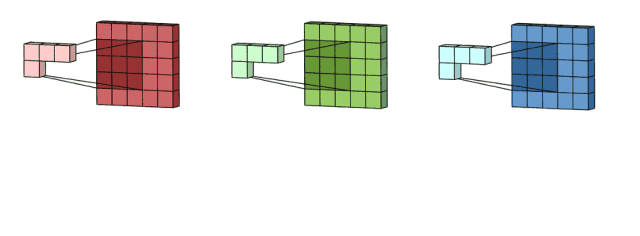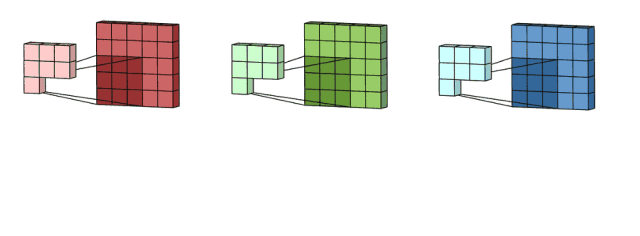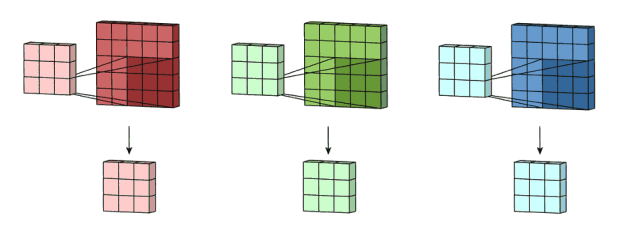
卷积核处理完数据后,形成了三个版本的处理结果,这时,filter再把它们加在一起形成一个总的通道。所以简而言之,卷积核处理的是不同通道的不同版本,而filter则是作为一个整体,产生一个整体的输出。
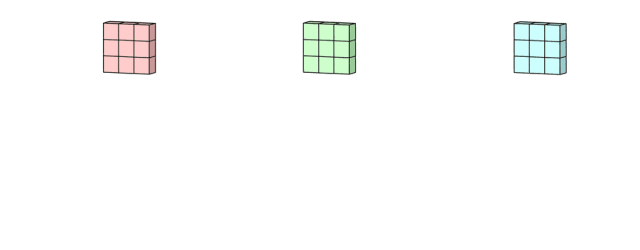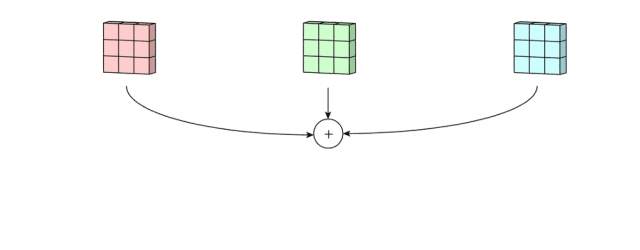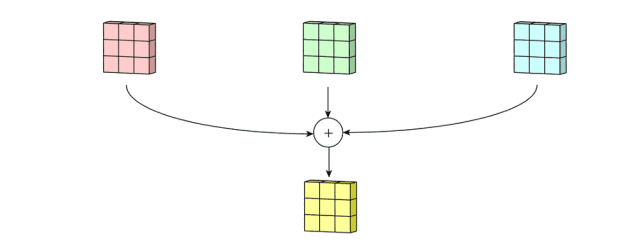
最后,还有偏置项。我们都知道每个filter输出后都要加上一个偏置项,那么为什么要放在这个位置呢?如果联系filter的作用,这一点不难理解,毕竟只有在这里,偏置项才能和filter一起作用,产生最终的输出通道。
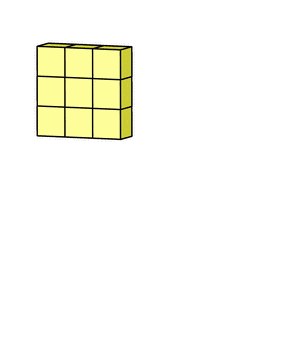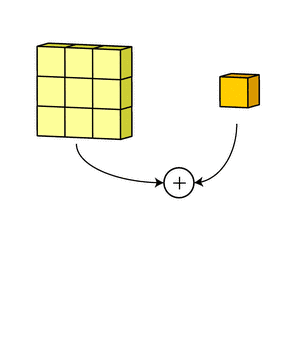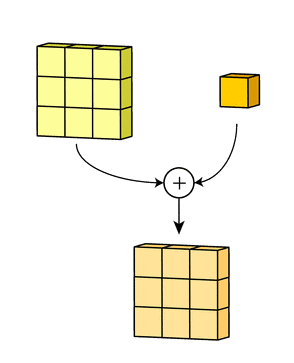
以上是单个filter的情况,但多个filter也是一样的工作原理:每个filter通过自己的卷积核集处理数据,形成一个单通道输出,加上偏置项后,我们得到了一个最终的单通道输出。如果存在多个filter,这时我们可以把这些最终的单通道输出组合成一个总输出,它的通道数就等于filter数。这个总输出经过非线性处理后,继续被作为输入馈送进下一个卷积层,然后重复上述过程。
2D卷积:直觉
卷积仍是线性变换
尽管上文已经讲解了卷积层的机制,但对比标准的前馈网络,我们还是很难在它们之间建立起联系。同样的,我们也无法解释为什么卷积可以进行缩放,以及它在图像数据上的处理效果为什么会那么好。
假设我们有一个4×4的输入,目标是把它转换成2×2的输出。这时,如果我们用的是前馈网络,我们会把这个4×4的输入重新转换成一个长度为16的向量,然后把这16个值输入一个有4个输出的密集连接层中。下面是这个层的权重矩阵W:

总而言之,有64个参数
虽然卷积的卷积核操作看起来很奇怪,但它仍然是一个带有等效变换矩阵的线性变换。如果我们在重构的4×4输入上使用一个大小为3的卷积核K,那么这个等效矩阵会变成:
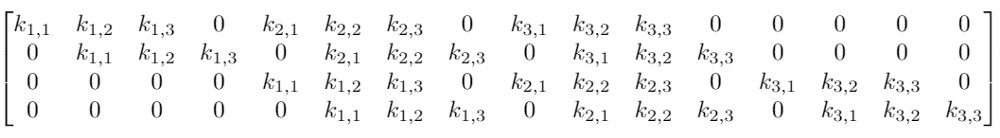
这里真的只有9个参数
注:虽然上面的矩阵是一个等效变换矩阵,但实际操作可能会不太一样。
可以发现,整个卷积仍然是线性变换,但与此同时,它也是一种截然不同的变换。相比前馈网络的64个参数,卷积得到的9个参数可以多次重复使用。由于权重矩阵中包含大量0权重,我们只会在每个输出节点看到选定数量的输入(卷积核的输入)。
而更高效的是,卷积的预定义参数可以被视为权重矩阵的先验。卷积核的大小、filter的数量,这些都是可以预定义的网络参数。当我们使用预训练模型进行图像分类时,我们可以把预先训练的网络参数作为当前的网络参数,并在此基础上训练自己的特征提取器。这会大大节省时间。
从这个意义上讲,虽然同为线性变换,卷积相比前馈网络的优势就可以被解释了。和随机初始化不同,使用预训练的参数允许我们只需要优化最终全连接层的参数,这意味着更好的性能。而大大削减参数数量则意味着更高的效率。
上图中我们只展示了把64个独立参数减少到9个共享参数,但在实际操作中,当我们从MNIST选择784幅224×224×3的图像时,它会有超过150,000个输入,也就是超过100亿个参数。相比之下,整个ResNet-50只有约2500万个参数。
因此,将一些参数固定为0可以大大提高效率。那么对比迁移学习,我们是怎么判断这些先验会产生积极效果的呢?
答案在于先前引导参数学习的特征组合。
局部性
在文章开头,我们就讨论过这么几点:
- 卷积核仅组合局部区域的几个像素,并形成一个输出。也就是说,输出特征只代表这一小块局部区域的输入特征。
- 卷积核会在“扫描”完整张图像后再生成输出矩阵。
因此,随着反向传播从分类节点开始往前推移,卷积核就可以不断调整权重,努力从一组本地输入中提取有效特征。另外,因为卷积核本身应用于整个图像,所以无论它学习的是哪个区域的特征,这些特征必须足够通用。
如果这是任何其他类型的数据,比如应用程序的安装序列号,卷积的这种操作完全不起作用。因为序列号虽然是一系列有顺序的数字,但他们彼此间没有共享的信息,也没有潜在联系。但在图像中,像素总是以一致的顺序出现,并且会始终对周围像素产生影响:如果所有附近的像素都是红色,那么我们的目标像素就很可能也是红色的。如果这个像素最终被证明存在偏差,不是红色的,那这个有趣的点就可能会被转换为特征。
通过对比像素和临近像素的差异来学习特征——这实际上是许多早期计算机视觉特征提取方法的基础。例如,对于边缘检测,我们可以使用Sobel edge detection:
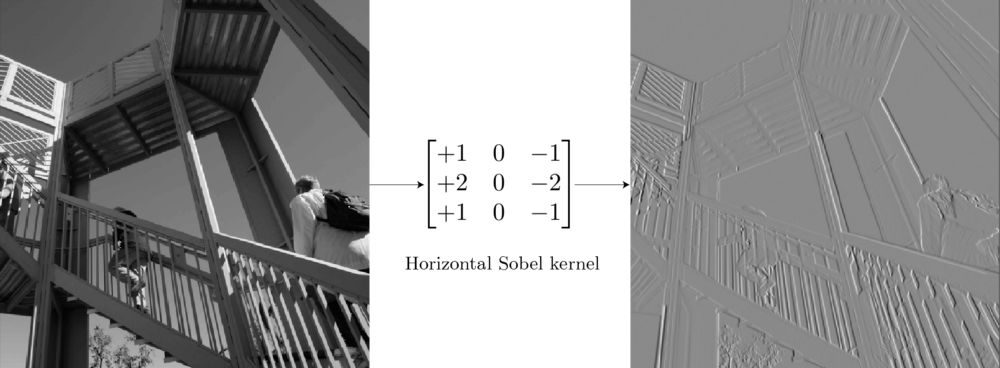
用于垂直边缘检测的Sobel算子
对于不包含边缘的网格(如天空),因为大多数像素都是相同的值,所以它的卷积核的总输出为0。对于具有垂直边缘的网格,边缘左侧和右侧的像素存在差异,所以卷积核的输出不为零,激活边缘区域。虽然这个卷积核一次只能扫描3×3的区域,提取其中的特征,但当它扫描完整幅图像后,它就有能力在图像中的任何位置检测全局范围内的某个特征。
那么深度学习和这种传统方法的区别是什么?对于图像数据的早期处理,我们确实可以用低级的特征检测器来检测图中的线条、边缘,那么,Sobel边缘算子的作用能否被卷积学习到?
深度学习研究的一个分支是研究神经网络模型可解释性,其中最强大的是使用了优化的特征可视化。它的思路很简单,就是通过优化图像来尽可能强烈地激活filter。这确实具有直观意义:如果优化后的图像完全被边缘填充,这其实就是filter本身正在寻找激活特征,并让自己被激活的强有力证据。

GoogLeNet第一个卷积层的3个不同通道的特征可视化,请注意,虽然它们检测到不同类型的边缘,但它们仍然是低级边缘检测器

GoogLeNet第二个、第三个卷积层的12个通道的特征可视化
这里要注意一点,卷积图像也是图像。卷积核是从图像左上角开始滑动的,相应的,它的输出仍将位于左上角。所以我们可以在这个卷积层上在做卷积,以提取更深层的特征可视化。
然而,无论我们的特征检测器如何深入,在没有任何进一步改变的情况下,它们仍将在非常小的图像块上运行。无论检测器有多深,它的大小就只有3×3,它是不可能检测到完整的脸部的。这是感受野(Receptive field)的问题。
感受野
无论是什么CNN架构,它们的基本设计就是不断压缩图像的高和宽,同时增加通道数量,也就是深度。如前所述,这可以通过池化和Stride来实现。局部性影响的是临近层的输入输出观察区域,而感受野决定的则是整个网络原始输入的观察区域。
步幅卷积背后的想法是我们只滑动固定距离的间隔,并跳过中间的网格。
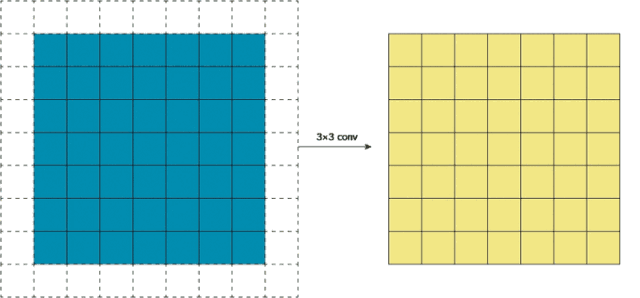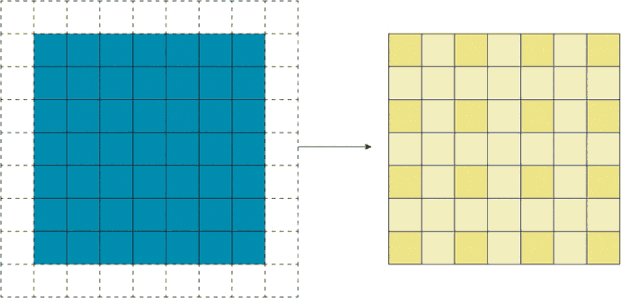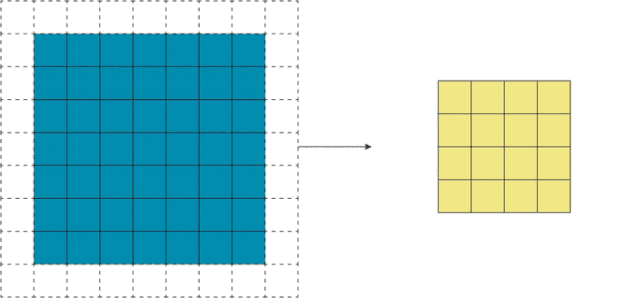
如上图所示,把stride调整为2后,卷积得到的输出大大缩小。这时,如果我们在这个输出的基础上做非线性激活,然后再上面再加一个卷积层,有趣的事就发生了。相比正常卷积得到的输出,3×3卷积核在这个步幅卷积输出上的感受野更大。
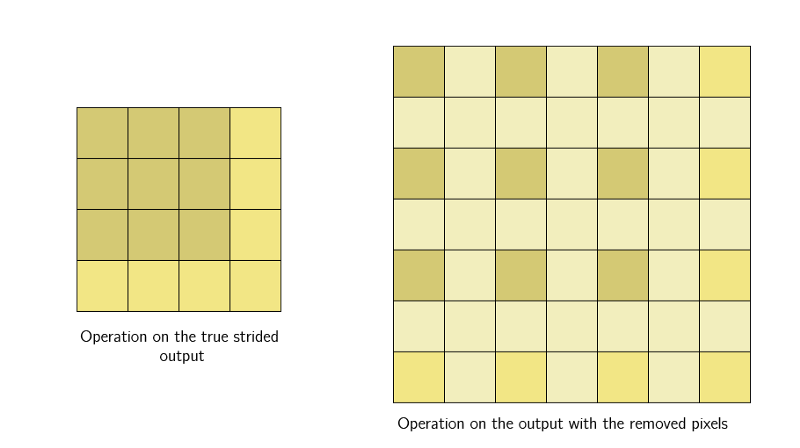
这是因为它的原始输入区域就比正常卷积的输入区域大,这会对后续特征提取产生影响。
这种感受野的扩大允许卷积层将低级特征(线条、边缘)组合成更高级别的特征(曲线、纹理),正如我们在mixed3a层中看到的那样。而随着我们添加更多Stride层,网络会显示出更多高级特征,如mixed4a、mixed5a。

通过检测低级特征,并使用它们来检测更高级别的特征,使其在视觉层次结构中向前发展,最终能够检测到整个视觉概念,如面部,鸟类,树木等。这就是卷积在图像数据上如此强大、高效的一个原因。
结论
现如今,CNN已经允许开发者们从构建简单的CV应用,到把它用于为复杂产品和服务提供技术动力,它既是照片库中用于检测人脸的小工具,也是临床医学中帮助医生筛查癌细胞的贴心助手。它们可能是未来计算机视觉的一个关键,当然,一些新的突破也可能即将到来。
但无论如何,有一件事是确定的:CNN是当今许多创新应用的核心,而且它们的效果绝对令人惊叹,这项技术本身也有掌握、了解的必要。
原文地址:towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
本文文字及图片出自 微信公众号
你也许感兴趣的:
- 如何入门PyTorch自然语言处理?
- TensorFlow,危!抛弃者正是谷歌自己
- 亚马逊机器学习服务Amazon SageMaker 又添九项新功能!
- “你们都很懂,从此我不说话了”,深度学习先驱Yann LeCun被骂关Twitter
- 趣图:对深度学习的考验
- 为什么深度学习这么容易被欺骗?
- 从 Google Trends,看各大深度学习框架使用热度
- 美团是如何基于深度学习实现图像的智能审核?
- 深度学习技术其实没那么美好
- 深度学习的局限性和未来















你对本文的反应是: