简单粗暴:用霰弹枪计算圆周率π
拿起自己的“小工具”对着它一通乱扫,枪眼越多越好,因为 π 的精度随着枪眼数量增加而提高。心情舒畅了以后,你需要统计一下板子上的枪眼个数,记得区分圆弧内外。

众所周知,圆周率 π=3.1415926…对于这个神奇的数字,我们可以利用“重要性抽样”(importance sampling)来计算,光听名字就觉得很厉害有木有。这种方法在仿真中非常重要,我们需要随机事件多次发生,让小概率事件也能频繁发生,从而降低方差,加快仿真速度。
而这种听起来就很厉害的方法是基于更加高大上的蒙特卡洛模拟法(Monte Carlo Simulations)的。使用这种方法模拟某一过程时,需要产生某一概率分布的随机变量,然后用统计方法把模型的数字特征估计出来,从而得到实际问题的数值解。
看懂了吗?看不懂也没什么关系,你只要学会下面的方法就可以了。
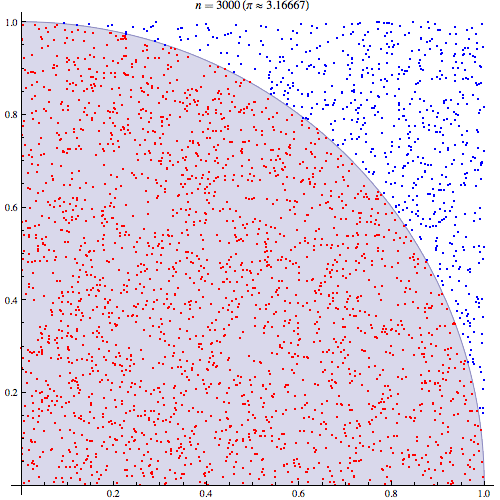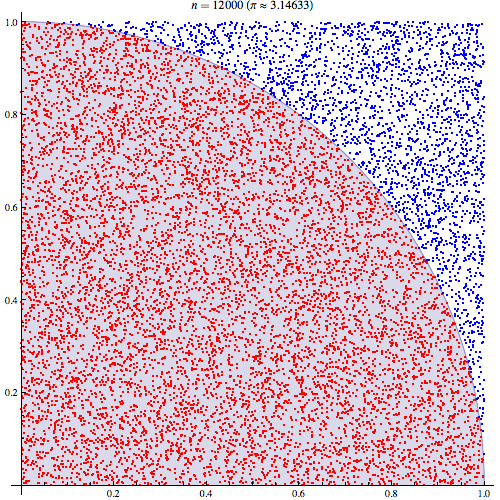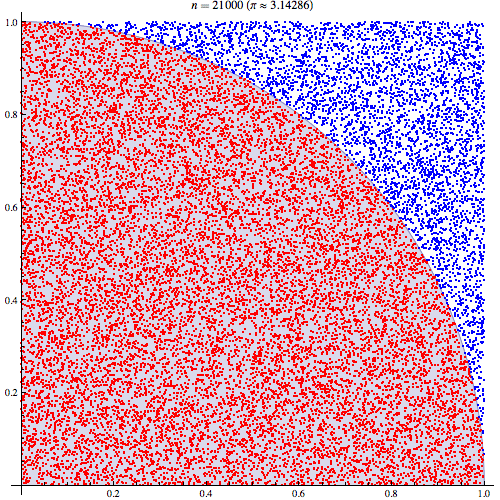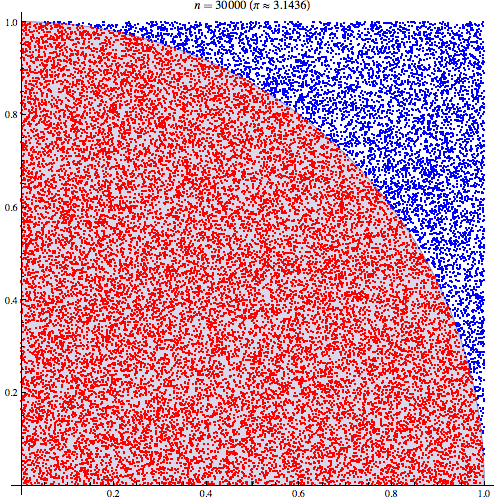
首先,挑一个心情极度不爽的日子,找块板子并裁成正方形,以正方形边长为半径画弧,然后把板子挂起来。完成这些准备工作之后,你就可以拿起自己的“小工具”对着它一通乱扫,枪眼越多越好,因为 π 的精度随着枪眼数量增加而提高。心情舒畅了以后,你需要统计一下板子上的枪眼个数,记得区分圆弧内外。
话又说回来,这么密密麻麻的枪眼要统计个数,还要区分圆弧内外,心情能舒畅多久?
需要记住的是,圆弧内的枪眼个数和整个正方形内的个数比值为 π/4(假设正方形边长为 1,则以 1 为半径的圆面积为 π,千万别问我这个结果是怎么得来的,1/4 圆的面积就是 π/4,而正方形的面积为 1),然后,狂点计算器吧。
事实上,真的有研究人员做过这个脑洞大过黑洞的实验,他们在 30857 个样本中得到了 3.13 这个还算不错的结果。

你也许感兴趣的:
- 不同的人生
- 小唐纳德求婚时,特朗普的视线
- 是什么阻止了你像这样编程?
- 指环王里的过去和现在
- 为他们高兴
- 同一个人,同一个姿势,只是衣服的纹理方向不同
- 想念 jQuery
- 金钱买不来幸福
- 唐纳德·特朗普总统在“年度风尚”选美大赛上与青少年模特合影(1991年)
- 西班牙王室与他们的先祖

假设整个正方形全部被弹孔覆盖,正方形的边长为一,则以正方形边长为半径的四分之一圆面积为pi/4……所以并没有什么神奇的地方……
你说的是已知条件,当然没有什么。精彩之处在于如何推出pi的数值…