图解堆排序,带你彻底了解清楚!
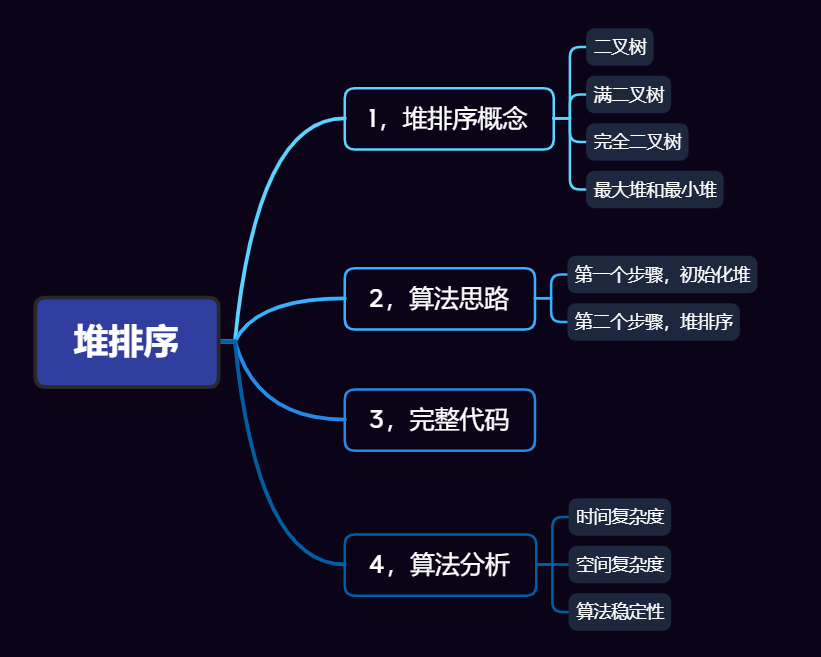
写在前面:大家好,我是时光。今天给大家带来的是排序算法中的堆排序,这种排序跟二叉树相关。我采用图解方式讲解,争取写透彻。话不多说,开始!思维导图:堆排序导图1,堆排序概念堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小
写在前面:
大家好,我是时光。
今天给大家带来的是排序算法中的堆排序,这种排序跟二叉树相关。我采用图解方式讲解,争取写透彻。话不多说,开始!
思维导图:
二叉树
特征:每个节点最多只有 2 个子节点(不存在度大于 2 的节点)
1.2,满二叉树
完全二叉树
完全二叉树:叶子节点全部都在最底的两层;最后一层只缺少右边的叶子节点,左边一定有叶子节点;除了最后一层,其他层的节点个数均达到最大值;
1.4,最大堆和最小堆
最大堆:堆顶是整个堆中最大元素
最小堆:堆顶是整个堆中最小元素
2,算法思路
我们先搞清楚这个堆排序思想,先把逻辑搞清楚,不着急写代码。
我们首先有一个无序数组,比方说
int[] arr={4,2,8,0,5,7,1,3,9};
既然用到堆,肯定先要将数组构建成二叉堆。需要对数组从小到大排序,则构建成最大堆;需要对数组从小到大排序,则构建成最小堆。
2.1,第一个步骤,初始化堆
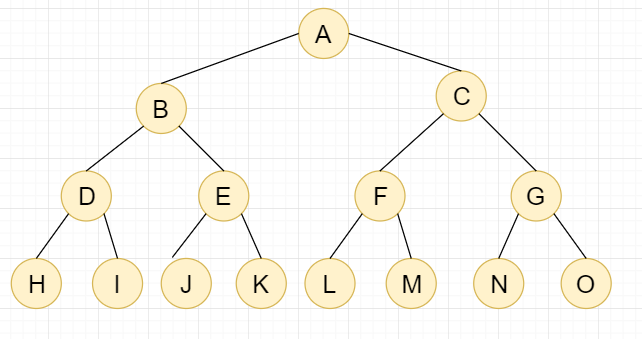
我们先来看看数组是如何存储二叉树的
数组存储完全二叉树
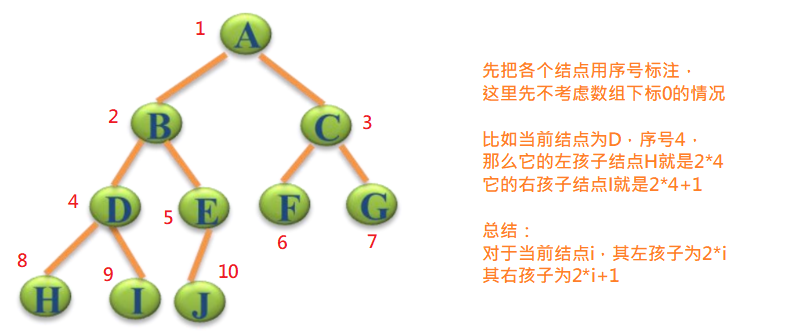
那么存储好之后,如何将二叉树构建成二叉堆呢?继续往下看
记录数组下标的二叉树
在这个图中,明显不满足最大堆的要求。我们先拿序号为 3,7,8 的三个节点来研究,i=3 的节点比 i=7 和 i=8 的节点都小,所以需要交换位置。注意此图是从 0 开始,也就是模拟数组下标从 0 开始。
怎么交换呢?很简单。我们看节点 0,设为当前节点index,那么它的lchild=index*2+1,它的rchild=index*2+2;注意下标从 0 开始。
//初始化堆
public static void HeapAdjust(int[] arr,int index,int len){
//先保存当前节点的下标
int max = index;
//保存左右孩子数组下标
int lchild = index*2+1;
int rchild = index*2+2;
//开始调整,左右孩子下标必须小于len,也就是确保数组不会越界
if(lchild<len && arr[lchild] > arr[max]){
max=lchild;
}
if(rchild<len && arr[rchild] > arr[max]){
max=rchild;
}
//若发生了交换,则max肯定不等于index了。此时max节点值需要与index节点值交换,上面交换索引值,这里交换节点值
if(max!=index){
int temp=arr[index];
arr[index]=arr[max];
arr[max]=temp;
//交换完之后需要再次对max进行调整,因为此时max有可能不满足最大堆
HeapAdjust(arr,max,len);
}
}
上面代码很好理解,中间的两个 if 语句就是交换节点索引值,只要有一个孩子节点大于index,就需要进行交换。若父节点index比两个孩子节点都大,那么就不需要交换了。
最后面的 if 语句是交换节点值,我们知道,只要index与lchild和rchild有交换,则index一定不等于max了!
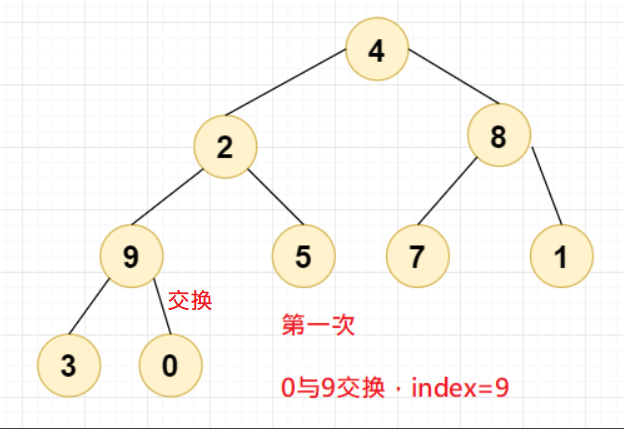
那为什么最后的if语句里面还要加上一个递归写法呢?我们举个例子就明白了,还是以上述数组为例,先看看一轮交换之后的样子:
第一次交换,0 与 9 交换,此时 Index=9;
2 与 9 交换
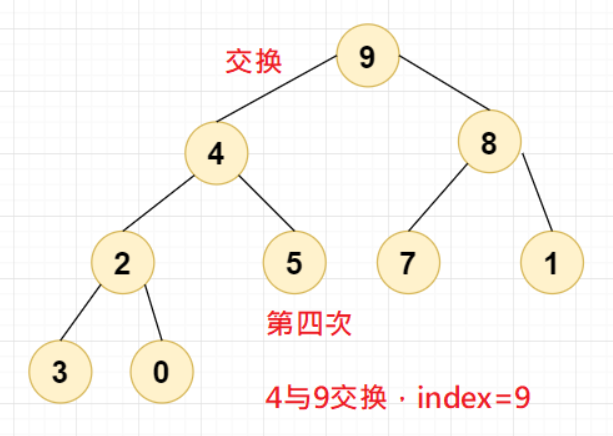
第四次交换,4 与 9 交换,此时
Index=9,第一轮交换到此结束。
初始化堆结束
2.2,第二个步骤,堆排序
堆排序的过程就是将堆顶元素(最大值或者最小值)与二叉堆的最末尾叶子节点进行调换,不停的调换,直到二叉堆的顺序变成从小到大或者从大到小,也就实现了我们的目的。
我们这里以最大堆的堆顶元素(最大元素)为例,最后调换的结果就是从小到大排序的结果。
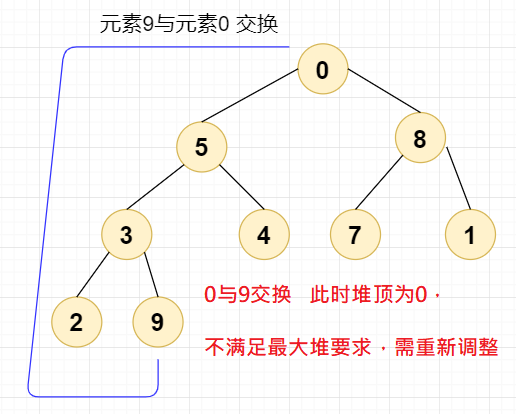
第一次交换,我们直接将元素 9 与元素 0 交换,此时堆顶元素为 0,设当前节点
index=0;
除元素 9 以外剩下的元素排序
代码:
/**
* 第二步,交换堆顶(最大)元素和二叉堆的最后一个叶子节点元素。目的是交换元素
* i从二叉堆的最后一个叶子节点元素开始,也就是len-1开始(数组下标从0开始)
*/
for(int i=len-1;i>=0;i--){
int temp=arr[i];
arr[i]=arr[0];
arr[0]=temp;
//交换完之后需要重新调整二叉堆,从头开始调整,此时Index=0
HeapAdjust(arr,0,i);
}
注意:这里有个小细节问题,前面我们写的初始化堆方法有三个参数,分别是数组arr,当前节点index以及数组长度len,如下:
HeapAdjust(int[] arr,int index,int len)
那么,为何不直接传入两个参数即可,数组长度直接用arr.length表示不就行了吗?初始化堆的时候是可以,但是后面在交换堆顶元素和末尾的叶子节点时,在对剩下的元素进行排序时,此时的数组长度可不是arr.length了,应该是变化的参数i,因为交换之后的元素(比如 9)就不计入堆中排序了,所以需要 3 个参数。
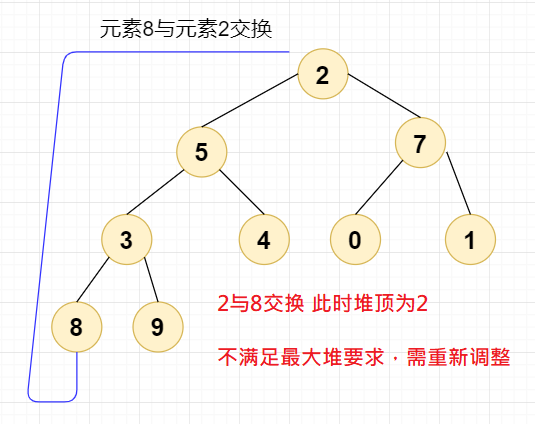
我们进行第二次交换,我们直接将元素 8 与元素 2 交换,此时堆顶元素为 2,设当前节点
index=2;
除元素 9 和 8 以外剩下的元素排序
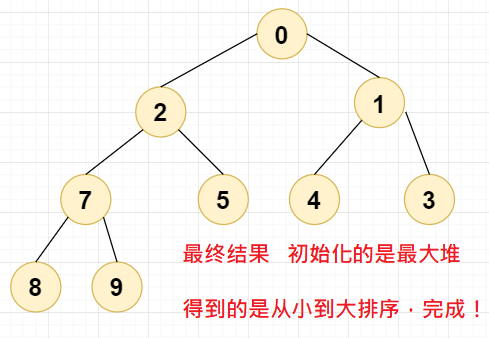
到这个时候,我们再重复上述步骤,不断调换堆顶和最末尾的节点元素即可,再不断地对剩下的元素进行排序,最后就能得到从小到大排序好的堆了,如下图所示,这就是我们想要的结果:
运行结果
4,算法分析
4.1,时间复杂度
建堆的时候初始化堆过程(HeapAdjust)是堆排序的关键,时间复杂度为O(log n),下面看堆排序的两个过程;
第一步,初始化堆,这一步时间复杂度是O(n);
第二步,交换堆顶元素过程,需要用到 n-1 次循环,且每一次都要用到(HeapAdjust),所以时间复杂度为((n-1)*log n)~O(nlog n);
最终时间复杂度:O(n)+O(nlog n),后者复杂度高于前者,所以堆排序的时间复杂度为 O(nlog n);
4.2,空间复杂度
空间复杂度是O(1),因为没有用到额外开辟的集合空间。
4.3,算法稳定性
堆排序是不稳定的,比方说二叉树[6a,8,13,6b],(这里的 6a 和 6b 数值上都是 6,只不过为了区别 6 所以这样)经过堆初始化后以及排序过后就变成[6b,6a,8,13];可见堆排序是不稳定的。
微信搜索公众号《程序员的时光》
好了,今天就先分享到这里了,下期继续给大家带来 排序算法面试内容!
更多干货、优质文章,欢迎关注我的原创技术公众号~
本文文字及图片出自 InfoQ

本文由 TecHug 分享,英文原文及文中图片来自 。
你也许感兴趣的:
- 雷蒙德·陈 旧事新说:当愤怒的客户要求与比尔·盖茨通话时
- 微软否认使用人工智能用Rust语言重写Windows 11
- 讨论:为什么Python能胜出?
- 使用 PostgreSQL 18 实现即时数据库克隆
- 我断开IPv4整整一周,只为理解IPv6过渡机制
- 我在地铁上编程
- Debian 的 Git 迁移计划
- Debian将龙芯LoongArch列为官方支持的架构
- Android对美国外部内容链接引入2-4美元安装费及10-20%分成政策
- 软件控制等级军事标准


你对本文的反应是: